目录
1. 离散化的概念
1.1 离散化的运用思路
1.2 离散化的方法
1.2.1 排序
1.2.2 确定一个元素离散化后的结果
1.3 案例分析
1.3.1
1.3.2 区间和 (来源:Acwing)
1. 离散化的概念
离散化,把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。
例如:
原数据:1,999,100000,15;处理后:1,3,4,2;
原数据:{100,200},{20,50000},{1,400};
处理后:{3,4},{2,6},{1,5};
1.1 离散化的运用思路
以下离散化均指整数保序的离散化。
根据离散化的定义,我们能够发现需要如果数据需要做离散化的处理,那么该数据的值域跨度是非常大的,但是分布很稀疏。因为值域的跨度相当大,自身并不能作为数组的下标保存对应的属性。但是如果只需要这些数据的相对属性,那么就可以对数据进行离散化处理。
1.2 离散化的方法
这里只讲常用的方法:重复元素离散化的结果相同。
我们只需要确保两个事情不变:
首先:保证离散化之后的数据尽可能地小而且非负。
其次:离散后的数据要保持原本的大小关系,原本相等的也要保持相等,否则就是错误的离散。
因此,找出原数据在序列中的序位 (可以直接理解为排第几) 就是离散化的关键。
1.2.1 排序
离散化就是确定找出原数据在序列中排第几嘛,因此我们直接对其排序就好了,排完序便可直接根据该数据所在位置的下标确定其离散化的结果。但是显然单单排序是不够的,如果原数据中有重复元素,那么相同的数据就会有不同的离散化结果,这是不被允许的。因此,对排好序的数组我们还要进行去重的操作。
假设原数组为 array。
对于C++:排序用sort,去重用unique,删除末尾重复的元素用erase,即:
array.erase(unique(array.begin(), array.end()), array.end())

对于C语言:用 qsort 排序,用双指针算法去重就行。
1.2.2 确定一个元素离散化后的结果
比如:将数据:1 5 3 2 2 3,进行排序,去重,删除后,得到结果:1 2 3 5,比如我们想要知道 5 离散化后的结果是多少,该怎么做呢?答案就是二分查找哦。5 对应的下标就是 5 离散化的结果。这里就是标准的二分查找模板。
二分查找请参考:http://t.csdn.cn/CVAGj
int binary_search1(int* nums, int numsSize, int target)
{
int l = 0, r = numsSize - 1;
while (l < r)
{
int mid = l + r >> 1;
if (nums[mid] >= target)
{
r = mid;
}
else
{
l = mid + 1;
}
}
return l;
}1.3 案例分析
1.3.1
题目描述:
现有数列 A1,A2,A3 ··· ,An,数列中可能有重复元素。现在要求输出该数列的离散化数列,重复元素离散化后的数字相同。
输入:
第一行,一个整数 n (1 <= n <= 10 ^ 5)
第二行,n个整数整数,每个整数的取值为:[-10^9, 10^9]。
输出:
一行,包括 n 个整数。表示数列对应的离散化数列,重复元素离散化后的数字相同。
样例输入:
6
1 23424 242 65466 242 0
样例输出:
1 3 2 4 2 0
int binary_search1(vector<int>& nums, int target)
{
int l = 0, r = nums.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (nums[mid] >= target)
{
r = mid;
}
else
{
l = mid + 1;
}
}
return l;
}
int main()
{
vector<int> array;
vector<int> a;
int n;
cin >> n;
int num;
for (int i = 0; i < n; i++)
{
scanf("%d", &num);
array.push_back(num);
a.push_back(num);
}
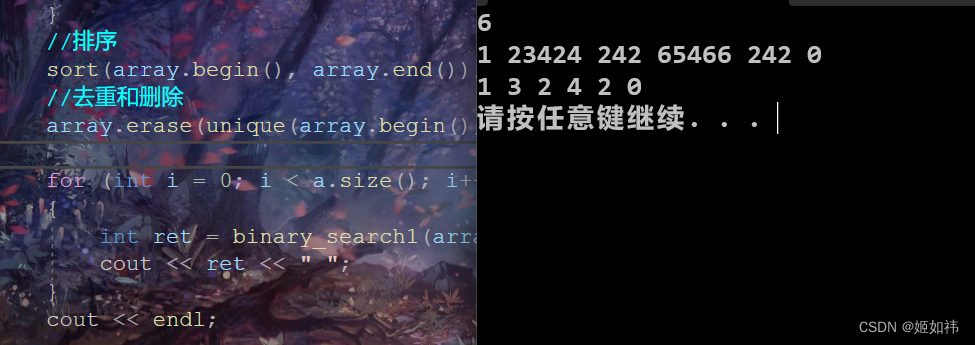
//排序
sort(array.begin(), array.end());
//去重和删除
array.erase(unique(array.begin(), array.end()), array.end());
for (int i = 0; i < a.size(); i++)
{
int ret = binary_search1(array, a[i]);
cout << ret << " ";
}
cout << endl;
system("pause");
return 0;
}
1.3.2 区间和 (来源:Acwing)
假定有一个无限长的数轴,数轴上每个坐标的数都是0.
现在我们首先进行 n 次操作,每次操作将某一位置 x 上的数加上 c 。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l, r] 之间所有数的和。
输入格式:
第一行包含两个整数 n 和 m。
接下来 n 行,包含两个整数 x 和 c。
再接下来 m 行,每行包含两个整数l 和 r。
输出格式:
共 m 行,每行输出一个询问中所求的区间内数字和。
数据范围:
-10 ^ 9 <= x <= 10 ^ 9 ,
1 <= n , m <= 10 ^ 5 ,
-10 ^ 9 <= l <= r <= 10 ^ 9 ,
-10000 <= c <= 10000
const int N = 300010;
//这里用来存在c的位置加上x 和每一次询问的区间,当然也可以用结构体
typedef pair<int, int> PI;
//在x的位置加上c不止一次,数组存
vector<PI> add;
//询问的区间不止一次,数组存
vector<PI> query;
//存所有添加的值c,需要离散化
vector<int>alls;
//保存离散化后的结果
int a[N];
//求区间和会用到前缀和的,创建一个前缀和数组
int s[N];
int n, m;
//这里离散化的值是从1开始的,为了对应求前缀和时也是从1开始
int binary_search1(int target)
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= target)
{
r = mid;
}
else
{
l = mid + 1;
}
}
return l + 1;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
int x, c;
cin >> x >> c;
//记录每一次添加的位置和值
add.push_back({ x,c });
//加上c的位置x是需要离散化的
alls.push_back(x);
}
//m次询问
for (int i = 0; i < m; i++)
{
int l, r;
cin >> l >> r;
//记录每一次询问
query.push_back({ l,r });
//输入的区间同样需要离散化
alls.push_back(l);
alls.push_back(r);
}
//排序,去重,删除
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
for (pair<int, int> i : add)
{
//将x位置加上c的x进行离散化
int x = binary_search1(i.first);
//a数组中的下标就代表离散化的值哈,值代表x的位置
a[x] += i.second;
}
//前缀和处理
for (int i = 1; i <= alls.size(); i++)
{
s[i] = s[i - 1] + a[i];
}
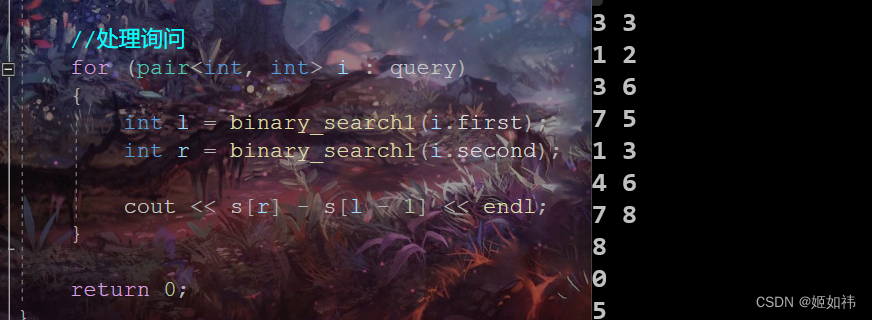
//处理询问
for (pair<int, int> i : query)
{
int l = binary_search1(i.first);
int r = binary_search1(i.second);
cout << s[r] - s[l - 1] << endl;
}
return 0;
}